11058. Chasing a
butterfly
On clear summer days, Nyusha loves to catch
butterflies in the fresh air. Today she came across a cunning butterfly: she
flew into the labyrinth and wanted to hide in it from Nyusha.
The labyrinth consists of n rooms,
numbered from 1 to n, some of which are connected by corridors. It is
known that between any two rooms there is a single path from the corridors. In
other words, the maze is a tree, and the number of corridors is n – 1.
The entrance to the labyrinth is located in the room number 1. We will call a leaf any
room of the labyrinth that is connected by a corridor to exactly one other room
and does not coincide with the root. In each of the leaves there is an exit
from the labyrinth. The butterfly flies from the entrance towards one of the
leaves. It flies at a constant speed and does not turn around. All corridors
have the same length, and in one minute the butterfly flies through one
corridor, moving to the next room.
To catch the butterfly, Nyusha decided to
call a few of her friends. Initially, each of the friends can be located in any of the rooms containing the exit. At the moment when the butterfly starts to fly from the
entrance to the labyrinth to one of the exits, each of the friends can start
moving from their room towards the entrance. Friends move at the same speed as
a butterfly. If one of the friends was at the same point (in the room or in the
middle of one of the corridors) with a butterfly, then the butterfly is considered to be caught. If the butterfly reaches the top
with the exit, without meeting any of the friends along the way, it will safely
flutter out of the maze and fly away to freedom.
Help Nyusha determine the minimum number of
friends she needs to be sure to catch the butterfly, no matter which exit it
flies to.
Input. The first line contains an integer n (2 ≤ n ≤ 200000) – the number of rooms in the maze.
The next n – 1 lines contain
descriptions of the corridors connecting the rooms. Each of these lines
contains two integers u and v (1 ≤ u, v ≤ n, u ≠ v) – numbers of rooms connected by the corridor. It is
guaranteed that the corridor structure is a tree.
Output. Print one integer – the minimum number of friends
needed to be sure to catch a butterfly.
|
Sample
input 1 |
Sample output 1 |
|
3 1 2 1 3 |
2 |
|
|
|
|
Sample
input 2 |
Sample output 2 |
|
4 1 2 2 3 2 4 |
1 |
SOLUTION
graphs – dfs
Algorithm analysis
Start a depth first
search from the vertex 1. For each vertex compute two values:
·
d[v] – distance from the
vertex 1 to v. If p is a
parent of v, then
d[v]
= d[p] + 1
·
h[v] – distance from the vertex
v to the nearest leaf in the subtree rooted at v. If to1,
to2, …, tok are sons of v, then
h[v]
= 1 + min(h[to1], h[to2], …, h[tok])
If v is a leaf
of the tree, let h[v]
= 0.
Start a second
depth first search. There
we’ll compute the answer res[v] for the vertex v: the
minimum number of friends that should be placed in some of the leaves of this
subtree in order to be guaranteed to catch a butterfly, provided that it
definitely flies to this subtree.
If h[v] ≤ d[v], then res[v] = 1. It is enough to put one friend in a leaf with a minimum
depth and he will reach the vertex v no later than the butterfly from
the root to v. Otherwise
if to1, to2, …, tok are
sons of v, then
res[v]
= res[to1] + res[to2] + … + res[tok]
If we don’t catch
the butterfly at v, then we should be ready to catch it in any of the
subtrees of v’s sons.
The answer to the problem will be the number res[1].
Example
For the first example (picture on the left), two friends are
required, which should be placed in two exits. A butterfly can fly from vertex
1 either to vertex 2 or to 3. But Nyusha’s friend will catch her in 2 and in 3.
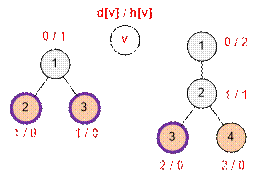
In the second example (picture on the right), one friend is
enough, who can be placed in any of the two exits – vertex number 3 or 4. In one minute, the butterfly will move from
vertex 1 to vertex 2. After 1 minute, the friend will be in vertex 2, where he
will catch a butterfly.
Consider the following example.
Nyusha needs three friends to catch a butterfly.
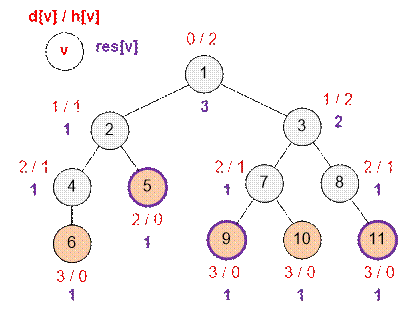
Algorithm realization
Declare an infinity constant and arrays.
#define INF 2000000000
vector<vector<int>
> g;
vector<int> d, h, res;
The
function dfs (v, p, cnt) performs a
depth-first search from the vertex v and returns the value h[v].
The ancestor of v is p. The distance from vertex 1 to v is
equal to cnt. For each vertex v we calculate the values d[v]
and h[v].
int dfs(int v, int p = -1, int cnt = 0)
{
The distance from vertex 1 to v is equal to cnt,
store it in d[v].
d[v] = cnt;
int height = INF;
Iterate over the sons of the vertex
v. Consider the edge v → to. If to is the same as v’s parent (to = p), then
move on to the next child.
for (int to : g[v])
if (to !=
p)
In
the variable height compute min(h[to1],
h[to2], …, h[tok]), where to1,
to2, …, tok are sons of v.
height = min(height, dfs(to, v, cnt + 1));
If height = INF, then v is a leaf and we set h[v] = 0.
Otherwise
rerturn h[v] = 1 + min(h[to1], h[to2],
…, h[tok]).
return h[v] =
(height == INF) ? 0 : 1 + height;
}
The function dfs2 (v, p) performs a depth-first search from
the vertex v and returns the value res[v]. The ancestor of v is p.
int dfs2(int v, int p = -1)
{
int s = 0;
Let to1,
to2, …, tok be the sons of v. In
the variable s compute the sum res[to1]
+ res[to2] + … + res[tok].
for (int to : g[v])
if (to != p)
{
dfs2(to, v);
s += res[to];
}
If h[v] ≤ d[v], its enough one friend, so res[v] = 1.
Otherwise res[v] = res[to1]
+ res[to2] + … + res[tok]
= s.
return res[v] = (h[v] <=
d[v]) ? 1 : s;
}
The main
part of the program. Read the input data. Construct a graph.
scanf("%d", &n);
g.resize(n + 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Initialize
the arrays.
d.resize(n + 1);
h.resize(n + 1);
res.resize(n + 1);
Run the
depth first searches. First dfs for each
vertex v finds the values of d[v] and h[v].
dfs(1);
dfs2(1);
Print the
answer – the least number of friends required to catch a butterfly.
printf("%lld\n", res[1]);